एक निश्चित अभिन्न अंग के लिए भागों द्वारा एकीकरण। समाकलन परिभाषित करें
भागों द्वारा एकीकरण सूत्र इस प्रकार दिखता है:
.
भागों द्वारा एकीकरण की विधि में इस सूत्र को लागू करना शामिल है। पर व्यावहारिक अनुप्रयोगयह ध्यान देने योग्य है कि यू और वी एकीकरण चर के कार्य हैं। मान लीजिए कि एकीकरण चर को x के रूप में निर्दिष्ट किया गया है (अभिन्न संकेतन के अंत में अंतर चिह्न d के बाद का प्रतीक)। तब u और v x के फलन हैं: u(x) और v(x) ।
तब
, .
और भागों द्वारा एकीकरण का सूत्र इस प्रकार है:
.
अर्थात्, इंटीग्रैंड फ़ंक्शन में दो फ़ंक्शन का उत्पाद शामिल होना चाहिए:
,
जिनमें से एक को हम यू के रूप में दर्शाते हैं: जी(एक्स) = यू, और दूसरे के लिए अभिन्न की गणना की जानी चाहिए (अधिक सटीक रूप से, एंटीडेरिवेटिव पाया जाना चाहिए):
, फिर dv = f(x) dx .
कुछ मामलों में f(x) = 1
. अर्थात् अभिन्न में
,
हम g(x) = u, x = v रख सकते हैं।
सारांश
तो, में यह विधि, भागों द्वारा एकीकरण सूत्र याद रखने और दो रूपों में लागू करने लायक है:
;
.
भागों द्वारा एकीकरण द्वारा गणना की गई इंटीग्रल
लघुगणक और व्युत्क्रम त्रिकोणमितीय (अतिशयोक्तिपूर्ण) कार्यों वाले समाकलन
लघुगणक और व्युत्क्रम त्रिकोणमितीय या अतिशयोक्तिपूर्ण कार्यों वाले इंटीग्रल को अक्सर भागों द्वारा एकीकृत किया जाता है। इस मामले में, जिस भाग में लघुगणक या व्युत्क्रम त्रिकोणमितीय (अतिशयोक्तिपूर्ण) फ़ंक्शन होते हैं उसे यू द्वारा दर्शाया जाता है, शेष भाग को डीवी द्वारा दर्शाया जाता है।
यहां ऐसे अभिन्नों के उदाहरण दिए गए हैं, जिनकी गणना भागों द्वारा एकीकरण की विधि द्वारा की जाती है:
, , , , , , .
एक बहुपद और पाप x, cos x या e x के गुणनफल वाले समाकलन
भागों द्वारा एकीकरण सूत्र का उपयोग करके, प्रपत्र के अभिन्न अंग पाए जाते हैं:
, , ,
जहाँ P(x) x में एक बहुपद है। एकीकृत करते समय, बहुपद P(x) को u, और e ax dx द्वारा निरूपित किया जाता है, कॉस एक्स डीएक्सया पाप कुल्हाड़ी dx- डीवी के माध्यम से।
यहां ऐसे अभिन्नों के उदाहरण दिए गए हैं:
, , .
भागों द्वारा एकीकरण की विधि का उपयोग करके अभिन्नों की गणना के उदाहरण
लघुगणक और व्युत्क्रम त्रिकोणमितीय कार्यों वाले अभिन्नों के उदाहरण
उदाहरण
अभिन्न की गणना करें:
विस्तृत समाधान
यहां इंटीग्रैंड में एक लघुगणक शामिल है। प्रतिस्थापन करना
तुम = एलएन एक्स,
डीवी = एक्स 2 डीएक्स.
तब
,
.
हम शेष अभिन्न की गणना करते हैं:
.
तब
.
गणना के अंत में, स्थिरांक C जोड़ना आवश्यक है अनिश्चितकालीन अभिन्न- यह सभी आदिमों का समुच्चय है। इसे मध्यवर्ती गणनाओं में भी जोड़ा जा सकता है, लेकिन यह केवल गणनाओं को अव्यवस्थित करेगा।
अधिक संक्षिप्त समाधान
आप समाधान को छोटे संस्करण में प्रस्तुत कर सकते हैं. ऐसा करने के लिए, आपको यू और वी के साथ प्रतिस्थापन करने की आवश्यकता नहीं है, लेकिन आप कारकों को समूहित कर सकते हैं और दूसरे फॉर्म में भागों के सूत्र द्वारा एकीकरण लागू कर सकते हैं।
.उत्तर
बहुपद और पाप x, cos x या ex के गुणनफल वाले अभिन्नों के उदाहरण
उदाहरण
अभिन्न की गणना करें:
.
समाधान
आइए हम विभेदक चिह्न के अंतर्गत घातांक का परिचय दें:
ई - एक्स डीएक्स = - ई - एक्स डी(-एक्स) = - डी(ई - एक्स).
आइए भागों द्वारा एकीकृत करें।
.
हम भागों द्वारा एकीकरण की विधि का भी उपयोग करते हैं।
.
.
.
अंततः हमारे पास है.
निम्नलिखित सूत्र कहा जाता है भागों सूत्र द्वारा एकीकरण अनिश्चितकालीन अभिन्न में:
भागों के सूत्र द्वारा एकीकरण को लागू करने के लिए, इंटीग्रैंड को दो कारकों में विभाजित किया जाना चाहिए। उनमें से एक को निरूपित किया जाता है यू, और शेष दूसरे कारक को संदर्भित करता है और द्वारा दर्शाया गया है डीवी. फिर विभेदन द्वारा हम पाते हैं ड्यूऔर एकीकरण - कार्य वी. उसी समय, के लिए यू डीवी- इंटीग्रैंड का ऐसा भाग जिसे आसानी से एकीकृत किया जा सके।
भागों द्वारा एकीकरण की विधि का उपयोग करना कब लाभदायक है? फिर कब इंटीग्रैंड में शामिल है :
1) - लॉगरिदमिक फ़ंक्शंस, साथ ही व्युत्क्रम त्रिकोणमितीय फ़ंक्शंस (उपसर्ग "चाप" के साथ), फिर, भागों द्वारा एकीकरण के दीर्घकालिक अनुभव के आधार पर, इन फ़ंक्शंस को निरूपित किया जाता है यू;
2) , , - ज्या, कोज्या और घातांक से गुणा पी(एक्स) x में एक मनमाना बहुपद है, तो इन फलनों को इसके द्वारा निरूपित किया जाता है डीवी, और बहुपद के माध्यम से है यू;
3) , , , , इस मामले में भागों द्वारा एकीकरण दो बार लागू किया जाता है।
आइए हम पहले मामले के उदाहरण का उपयोग करके भागों द्वारा एकीकरण की विधि का मूल्य समझाएं। मान लीजिए कि अभिन्न चिह्न के अंतर्गत अभिव्यक्ति में एक लघुगणकीय फ़ंक्शन शामिल है (यह उदाहरण 1 होगा)। भागों द्वारा एकीकरण का उपयोग करके, इस तरह के एक अभिन्न अंग को केवल बीजगणितीय कार्यों (अक्सर एक बहुपद) के अभिन्न अंग की गणना करने के लिए कम किया जाता है, यानी, इसमें लॉगरिदमिक या व्युत्क्रम त्रिकोणमितीय फ़ंक्शन शामिल नहीं होता है। पाठ की शुरुआत में दिए गए भागों द्वारा एकीकरण सूत्र का उपयोग करना
हम पहले पद में (अभिन्न के बिना) एक लघुगणकीय फ़ंक्शन प्राप्त करते हैं, और दूसरे पद में (अभिन्न चिह्न के तहत) एक फ़ंक्शन प्राप्त करते हैं जिसमें लघुगणक नहीं होता है। एक बीजगणितीय फलन का समाकलन उस समाकलन की तुलना में बहुत सरल होता है जिसके चिह्न के अंतर्गत लघुगणकीय या व्युत्क्रम अलग से या बीजगणितीय गुणनखंड के साथ पाया जाता है त्रिकोणमितीय फलन.
इस प्रकार, का उपयोग कर भागों के सूत्रों द्वारा एकीकरण एकीकरण तुरंत नहीं किया जाता है: किसी दिए गए अभिन्न को ढूंढना दूसरे को खोजने के लिए कम हो जाता है। भागों के सूत्र द्वारा एकीकरण का अर्थ यह है कि इसके अनुप्रयोग के परिणामस्वरूप, नया अभिन्न अंग सारणीबद्ध हो जाता है या कम से कम मूल की तुलना में सरल हो जाता है।
भागों द्वारा एकीकरण की विधि दो कार्यों के उत्पाद को अलग करने के लिए सूत्र के उपयोग पर आधारित है:
तो इसे फॉर्म में लिखा जा सकता है
जो पाठ के आरंभ में ही दिया गया था।
फ़ंक्शन को एकीकृत करके खोजते समय वीइसके लिए प्रतिअवकलन फलनों का एक अनंत सेट प्राप्त होता है। भागों के सूत्र द्वारा एकीकरण को लागू करने के लिए, आप उनमें से कोई भी ले सकते हैं, और इसलिए वह जो एक मनमाना स्थिरांक से मेल खाता है साथ, शून्य के बराबर. इसलिए, फ़ंक्शन ढूंढते समय वीमनमाना स्थिरांक साथदर्ज नहीं किया जाना चाहिए.
भागों द्वारा एकीकरण की विधि का एक बहुत ही विशेष अनुप्रयोग है: इसका उपयोग अभिन्न चिह्न के तहत कार्यों की डिग्री को कम करने के लिए आवश्यक होने पर एंटीडेरिवेटिव कार्यों को खोजने के लिए आवर्ती सूत्रों को प्राप्त करने के लिए किया जा सकता है। डिग्री को कम करना तब आवश्यक होता है जब उदाहरण के लिए, दूसरे और उनके उत्पादों से अधिक शक्तियों के लिए साइन और कोसाइन जैसे कार्यों के लिए कोई सारणीबद्ध अभिन्न अंग नहीं होते हैं। आवर्ती सूत्र पिछले सदस्य के माध्यम से अनुक्रम के अगले सदस्य को खोजने का एक सूत्र है। संकेतित मामलों के लिए, लक्ष्य को क्रमिक रूप से डिग्री कम करके प्राप्त किया जाता है। इसलिए, यदि समाकलन x की चौथी घात के लिए एक ज्या है, तो भागों द्वारा एकीकृत करके आप तीसरी घात के लिए ज्या के समाकलन के लिए एक सूत्र पा सकते हैं, इत्यादि। इस पाठ का अंतिम पैराग्राफ वर्णित कार्य के लिए समर्पित है।
भागों द्वारा एकीकरण को एक साथ लागू करना
उदाहरण 1. भागों द्वारा एकीकरण की विधि का उपयोग करके अनिश्चितकालीन अभिन्न खोजें:
समाधान। एकीकृत अभिव्यक्ति में - लघुगणक, जिसे, जैसा कि हम पहले से ही जानते हैं, उचित रूप से दर्शाया जा सकता है यू. ऐसा हमारा विश्वास है , ।
हम पाते हैं (जैसा कि सैद्धांतिक संदर्भ के स्पष्टीकरण में पहले ही उल्लेख किया गया है, हम तुरंत पहले पद में (एक अभिन्न अंग के बिना) एक लघुगणकीय फ़ंक्शन प्राप्त करते हैं, और एक फ़ंक्शन जिसमें दूसरे पद में एक लघुगणक शामिल नहीं होता है (अभिन्न चिह्न के तहत):

और फिर लघुगणक...
उदाहरण 2.अनिश्चितकालीन अभिन्न खोजें:
समाधान। होने देना , ।
लघुगणक वर्ग में मौजूद है. इसका मतलब यह है कि इसे एक जटिल कार्य के रूप में विभेदित करने की आवश्यकता है। हम देखतें है
,
.
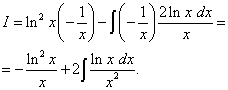
हम फिर से भागों द्वारा दूसरा अभिन्न पाते हैं और पहले से उल्लिखित लाभ प्राप्त करते हैं (पहले पद में (अभिन्न के बिना) एक लघुगणकीय फ़ंक्शन होता है, और दूसरे पद में (अभिन्न चिह्न के तहत) एक फ़ंक्शन होता है जिसमें कोई शामिल नहीं होता है लघुगणक).


हम मूल अभिन्न पाते हैं:

उदाहरण 3.
समाधान। लघुगणक की तरह चापस्पर्शरेखा को बेहतर तरीके से दर्शाया जाता है यू. तो चलो , ।
तब ,
.
भागों द्वारा एकीकरण सूत्र को लागू करने पर, हम प्राप्त करते हैं:
![]()
हम एक चर को बदलकर दूसरा अभिन्न अंग पाते हैं।


वेरिएबल पर लौटना एक्स, हम पाते हैं
![]() .
.
हम मूल अभिन्न पाते हैं:
![]() .
.
उदाहरण 4. भागों द्वारा एकीकरण की विधि का उपयोग करके अनिश्चितकालीन अभिन्न अंग ज्ञात करें:
समाधान। घातांक को इससे निरूपित करना बेहतर है डीवी. हमने इंटीग्रैंड को दो कारकों में विभाजित किया है। ऐसा मानना
उदाहरण 5. भागों द्वारा एकीकरण की विधि का उपयोग करके अनिश्चितकालीन अभिन्न अंग ज्ञात करें:
![]() .
.
समाधान। होने देना , । तब , ।
भागों द्वारा एकीकरण सूत्र (1) का उपयोग करके, हम पाते हैं:
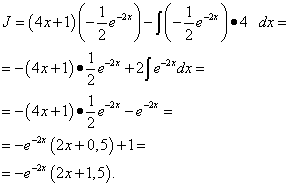
उदाहरण 6.भागों द्वारा एकीकरण द्वारा अनिश्चितकालीन अभिन्न खोजें:
समाधान। घातांक की तरह ज्या को भी आसानी से दर्शाया जा सकता है डीवी. होने देना , ।
भागों द्वारा एकीकरण सूत्र का उपयोग करके हम पाते हैं:

हम फिर से भागों द्वारा एकीकरण लागू करते हैं
उदाहरण 10.भागों द्वारा एकीकरण द्वारा अनिश्चितकालीन अभिन्न खोजें:
![]() .
.
समाधान। जैसा कि हर किसी में होता है समान मामले, कोज्या को इससे निरूपित करना सुविधाजनक है डीवी. हम दर्शाते हैं , .
तब ![]() ,
.
,
.
भागों द्वारा एकीकरण सूत्र का उपयोग करके, हम प्राप्त करते हैं:
हम दूसरे कार्यकाल में भागों द्वारा एकीकरण भी लागू करते हैं। हम दर्शाते हैं , .
इन नोटेशनों का उपयोग करते हुए, हम उल्लिखित शब्द को एकीकृत करते हैं:

अब हम आवश्यक अभिन्न पाते हैं:

जिन अभिन्नों को भागों द्वारा एकीकरण की विधि द्वारा हल किया जा सकता है, उनमें वे भी हैं जो सैद्धांतिक भाग में उल्लिखित तीन समूहों में से किसी में शामिल नहीं हैं, जिनके लिए अभ्यास से ज्ञात होता है कि इसे निरूपित करना बेहतर है यू, और किस माध्यम से डीवी. इसलिए, इन मामलों में, आपको सुविधा के विचार का उपयोग करने की आवश्यकता है, जो पैराग्राफ "भागों द्वारा एकीकरण की विधि का सार" में भी दिया गया है: के लिए यूकिसी को इंटीग्रैंड का एक हिस्सा लेना चाहिए जो भेदभाव के दौरान अधिक जटिल नहीं हो जाता है, लेकिन डीवी- इंटीग्रैंड का ऐसा भाग जिसे आसानी से एकीकृत किया जा सके। इस पाठ का अंतिम उदाहरण ऐसे ही एक अभिन्न का समाधान है।
एक निश्चित अभिन्न अंग द्वारा से सतत कार्य एफ(एक्स) अंतिम खंड पर [ ए, बी] (जहाँ ) इस खंड पर इसके कुछ प्रतिअवकलजों की वृद्धि है। (सामान्य तौर पर, यदि आप अनिश्चितकालीन अभिन्न अंग के विषय को दोहराते हैं तो समझना काफी आसान हो जाएगा) इस मामले में, संकेतन का उपयोग किया जाता है
जैसा कि नीचे दिए गए ग्राफ़ में देखा जा सकता है (एंटीडेरिवेटिव फ़ंक्शन की वृद्धि को इसके द्वारा दर्शाया गया है), निश्चित समाकलन या तो सकारात्मक हो सकता है या ऋणात्मक संख्या (इसकी गणना ऊपरी सीमा में प्रतिअवकलन के मूल्य और निचली सीमा में इसके मूल्य के बीच अंतर के रूप में की जाती है, अर्थात एफ(बी) - एफ(ए)).

नंबर एऔर बीक्रमशः एकीकरण की निचली और ऊपरी सीमाएँ कहलाती हैं, और खंड [ ए, बी] - एकीकरण का खंड।
इस प्रकार, यदि एफ(एक्स) - के लिए कुछ प्रतिव्युत्पन्न कार्य एफ(एक्स), फिर, परिभाषा के अनुसार,
![]() (38)
(38)
समानता (38) कहलाती है न्यूटन-लीबनिज सूत्र . अंतर एफ(बी) – एफ(ए) संक्षेप में इस प्रकार लिखा गया है:
इसलिए, हम न्यूटन-लीबनिज सूत्र इस प्रकार लिखेंगे:
![]() (39)
(39)
आइए हम सिद्ध करें कि निश्चित समाकलन इस बात पर निर्भर नहीं करता कि इसकी गणना करते समय समाकलन का कौन सा प्रतिअवकलन लिया जाता है। होने देना एफ(एक्स) और एफ( एक्स) इंटीग्रैंड के मनमाने एंटीडेरिवेटिव हैं। चूँकि ये एक ही फ़ंक्शन के प्रतिअवकलज हैं, इसलिए इनमें एक स्थिर पद का अंतर होता है: Ф( एक्स) = एफ(एक्स) + सी. इसीलिए

इससे यह स्थापित होता है कि खंड पर [ ए, बी] फ़ंक्शन के सभी एंटीडेरिवेटिव की वृद्धि एफ(एक्स) मेल खाना।
इस प्रकार, एक निश्चित अभिन्न की गणना करने के लिए, पूर्णांक के किसी भी प्रतिअवकलन को खोजना आवश्यक है, अर्थात। सबसे पहले आपको अनिश्चितकालीन अभिन्न को खोजने की आवश्यकता है। स्थिर साथ बाद की गणनाओं से बाहर रखा गया। फिर न्यूटन-लीबनिज़ फॉर्मूला लागू किया जाता है: ऊपरी सीमा का मान एंटीडेरिवेटिव फ़ंक्शन में प्रतिस्थापित किया जाता है बी , आगे - निचली सीमा का मूल्य ए और अंतर की गणना की जाती है एफ(बी) - एफ(ए) . परिणामी संख्या एक निश्चित पूर्णांक होगी।.
पर ए = बीपरिभाषा के अनुसार स्वीकृत
उदाहरण 1।
समाधान। सबसे पहले, आइए अनिश्चितकालीन अभिन्न अंग खोजें:
न्यूटन-लीबनिज़ सूत्र को प्रतिअवकलन पर लागू करना
(पर साथ= 0), हमें मिलता है
![]()
हालाँकि, एक निश्चित अभिन्न की गणना करते समय, यह बेहतर है कि प्रतिअवकलन को अलग से न खोजा जाए, बल्कि अभिन्न को तुरंत फॉर्म (39) में लिखा जाए।
उदाहरण 2.निश्चित अभिन्न की गणना करें
समाधान। सूत्र का उपयोग करना
![]()
![]()
निश्चित अभिन्न के गुण
प्रमेय 2.निश्चित अभिन्न का मान एकीकरण चर के पदनाम पर निर्भर नहीं करता है, अर्थात।
![]() (40)
(40)
होने देना एफ(एक्स) - के लिए प्रतिअवकलन एफ(एक्स). के लिए एफ(टी) प्रतिअवकलन एक ही कार्य है एफ(टी), जिसमें स्वतंत्र चर को केवल अलग ढंग से नामित किया गया है। इस तरह,
![]()
सूत्र (39) के आधार पर, अंतिम समानता का अर्थ अभिन्नों की समानता है
प्रमेय 3.अचर गुणनखंड को निश्चित समाकलन के चिह्न से निकाला जा सकता है, अर्थात।
![]() (41)
(41)
प्रमेय 4.कार्यों की एक सीमित संख्या के बीजीय योग का निश्चित समाकलन इन कार्यों के निश्चित समाकलों के बीजगणितीय योग के बराबर होता है, अर्थात।
 (42)
(42)
प्रमेय 5.यदि एकीकरण के एक खंड को भागों में विभाजित किया जाता है, तो पूरे खंड पर निश्चित अभिन्न अंग उसके भागों पर निश्चित अभिन्नों के योग के बराबर होता है, अर्थात। अगर
![]() (43)
(43)
प्रमेय 6.एकीकरण की सीमाओं को पुनर्व्यवस्थित करने पर, निश्चित अभिन्न का निरपेक्ष मान नहीं बदलता है, बल्कि केवल उसका चिह्न बदलता है, अर्थात।
![]() (44)
(44)
प्रमेय 7(माध्य मान प्रमेय)। समाकलन परिभाषित करें उत्पाद के बराबरइसके अंदर किसी बिंदु पर इंटीग्रैंड के मूल्य से एकीकरण के खंड की लंबाई, अर्थात।
![]() (45)
(45)
प्रमेय 8.यदि एकीकरण की ऊपरी सीमा निचली सीमा से अधिक है और समाकलन गैर-नकारात्मक (सकारात्मक) है, तो निश्चित समाकलन भी गैर-नकारात्मक (सकारात्मक) है, अर्थात। अगर

प्रमेय 9.यदि एकीकरण की ऊपरी सीमा निचली सीमा से अधिक है और कार्य निरंतर हैं, तो असमानता
शब्द दर शब्द एकीकृत किया जा सकता है, अर्थात।
![]() (46)
(46)
निश्चित समाकलन के गुण समाकलन की प्रत्यक्ष गणना को सरल बनाना संभव बनाते हैं।
उदाहरण 5.निश्चित अभिन्न की गणना करें
![]()
प्रमेय 4 और 3 का उपयोग करते हुए, और प्रतिअवकलन ज्ञात करते समय - तालिका समाकलन (7) और (6), हम प्राप्त करते हैं

परिवर्तनीय ऊपरी सीमा के साथ निश्चित अभिन्न अंग
होने देना एफ(एक्स) - खंड पर निरंतर [ ए, बी] फ़ंक्शन, और एफ(एक्स) इसका प्रतिअवकलन है। निश्चित अभिन्न पर विचार करें
![]() (47)
(47)
और के माध्यम से टीएकीकरण चर को निर्दिष्ट किया गया है ताकि इसे ऊपरी सीमा के साथ भ्रमित न किया जाए। जब यह बदलता है एक्सनिश्चित समाकलन (47) भी बदलता है, अर्थात्। यह एकीकरण की ऊपरी सीमा का एक कार्य है एक्स, जिसे हम निरूपित करते हैं एफ(एक्स), अर्थात।
![]() (48)
(48)
आइए हम सिद्ध करें कि फलन एफ(एक्स) के लिए एक प्रतिअवकलन है एफ(एक्स) = एफ(टी). वास्तव में, विभेद करना एफ(एक्स), हम पाते हैं

क्योंकि एफ(एक्स) - के लिए प्रतिअवकलन एफ(एक्स), ए एफ(ए) एक स्थिर मान है.
समारोह एफ(एक्स) - में से एक असीमित संख्याके लिए प्रतिअवकलज एफ(एक्स), अर्थात् वह जो एक्स = एशून्य हो जाता है. यदि हम समानता (48) में रखते हैं तो यह कथन प्राप्त होता है एक्स = एऔर पिछले पैराग्राफ के प्रमेय 1 का उपयोग करें।
भागों द्वारा एकीकरण की विधि तथा चर के परिवर्तन की विधि द्वारा निश्चित अभिन्नों की गणना
![]()
जहां, परिभाषा के अनुसार, एफ(एक्स) - के लिए प्रतिअवकलन एफ(एक्स). यदि हम वेरिएबल को इंटीग्रैंड में बदलते हैं
तो, सूत्र (16) के अनुसार, हम लिख सकते हैं
इस अभिव्यक्ति में
के लिए प्रतिव्युत्पन्न कार्य
वास्तव में, इसका व्युत्पन्न, के अनुसार जटिल कार्यों के विभेदन का नियम, बराबर है

माना α और β वेरिएबल के मान हैं टी, जिसके लिए फ़ंक्शन
तदनुसार मान लेता है एऔर बी, अर्थात।

लेकिन, न्यूटन-लीबनिज सूत्र के अनुसार, अंतर एफ(बी) – एफ(ए) वहाँ है
भागों द्वारा एकीकरण क्या है? इस प्रकार के एकीकरण में महारत हासिल करने के लिए, आइए सबसे पहले किसी उत्पाद के व्युत्पन्न को याद करें:
$((\left(f\cdot g \right))^(\ prime ))=(f)"\cdot g+f\cdot (g)"$
प्रश्न उठता है: अभिन्नों का इससे क्या लेना-देना है? आइए अब इस समीकरण के दोनों पक्षों को एकीकृत करें। तो चलिए इसे लिखते हैं:
$\int(((\left(f\cdot g \right))^(\ prime ))\text(d)x=)\int((f)"\cdot g\,\text(d)x+\ int(f\cdot (g)"\,\text(d)x))$
लेकिन स्ट्रोक का प्रतिव्युत्पन्न क्या है? यह केवल फ़ंक्शन ही है, जो स्ट्रोक के अंदर है। तो चलिए इसे लिखते हैं:
$f\cdot g=\int((f)"\cdot g\,\text(d)x+\int(f\cdot (g)"\,\text(d)x))$
में दिया गया समीकरणमैं शब्द को व्यक्त करने का प्रस्ताव करता हूं। हमारे पास है:
$\int((f)"\cdot g\,\text(d)x=f\cdot g-\int(f\cdot (g)"\,\text(d)x))$
यह वही है भागों सूत्र द्वारा एकीकरण. इस प्रकार, हम अनिवार्य रूप से व्युत्पन्न और फ़ंक्शन का आदान-प्रदान कर रहे हैं। यदि प्रारंभ में हमारे पास एक स्ट्रोक का एक अभिन्न अंग था जिसे किसी चीज़ से गुणा किया गया था, तो हमें एक स्ट्रोक से गुणा किए गए किसी नए चीज़ का एक अभिन्न अंग मिलता है। बस यही नियम है. पहली नज़र में, यह सूत्र जटिल और अर्थहीन लग सकता है, लेकिन वास्तव में, यह गणनाओं को बहुत सरल बना सकता है। चलो देखते हैं।
अभिन्न गणना के उदाहरण
समस्या 1. गणना करें:
\[\int(\ln x\,\text(d)x)\]\[\]
आइए लघुगणक से पहले 1 जोड़कर अभिव्यक्ति को फिर से लिखें:
\[\int(\ln x\,\text(d)x)=\int(1\cdot \ln x\,\text(d)x)\]
हमें ऐसा करने का अधिकार है क्योंकि न तो संख्या और न ही कार्य बदलेगा। आइए अब इस अभिव्यक्ति की तुलना हमारे सूत्र में लिखी गई बातों से करें। $(f)"$ की भूमिका 1 है, इसलिए हम लिखते हैं:
$\begin(संरेखित करें)& (f)"=1\दायां तीर f=x \\& g=\ln x\दायां तीर (g)"=\frac(1)(x) \\\end(संरेखित)$
ये सभी फ़ंक्शन तालिकाओं में हैं. अब जब हमने अपनी अभिव्यक्ति में शामिल सभी तत्वों का वर्णन कर लिया है, तो हम भागों द्वारा एकीकरण के सूत्र का उपयोग करके इस अभिन्न को फिर से लिखेंगे:
\[\begin(संरेखित करें)& \int(1\cdot \ln x\,\text(d)x)=x\ln x-\int(x\cdot \frac(1)(x)\text(d) )x)=x\ln x-\int(\text(d)x)= \\& =x\ln x-x+C=x\left(\ln x-1 \right)+C \\\ अंत(संरेखित करें)\]
बस, अभिन्न मिल गया।
समस्या 2. गणना करें:
$\int(x((\text(e))^(-x))\,\text(d)x=\int(x\cdot ((e)^(-x))\,\text(d )x))$
यदि हम $x$ को व्युत्पन्न के रूप में लेते हैं, जिससे अब हमें प्रतिअवकलन खोजने की आवश्यकता है, तो हमें $((x)^(2))$ मिलेगा, और अंतिम अभिव्यक्ति में $((x)^(2) होगा )( (\text(e))^(-x))$.
जाहिर है, समस्या सरल नहीं है, इसलिए हम अभिन्न चिह्न के तहत कारकों की अदला-बदली करते हैं:
$\int(x\cdot ((\text(e))^(-x))\,\text(d)x)=\int(((\text(e))^(-x))\cdot x\,\text(d)x)$
आइए अब संकेतन का परिचय दें:
$(f)"=((\text(e))^(-x))\राइटएरो f=\int(((\text(e))^(-x))\,\text(d)x) =-((\text(e))^(-x))$
आइए $((\text(e))^(-x))$ में अंतर करें:
$((\left(((\text(e))^(-x)) \right))^(\ prime ))=((\text(e))^(-x))\cdot ((\ बाएँ(-x \दाएँ))^(\प्रधान ))=-((\text(e))^(-x))$
दूसरे शब्दों में, पहले ऋण को जोड़ा जाता है और फिर दोनों पक्षों को एकीकृत किया जाता है:
\[\begin(संरेखित)& ((\left(((\text(e))^(-x)) \right))^(\प्राइम ))=-((\text(e))^(- x))\दायाँ तीर ((\text(e))^(-x))=-((\left(((\text(e))^(-x)) \right))^(\प्राइम )) \\& \int(((\text(e))^(-x))\,\text(d)x)=-\int(((\left(((\text(e))^(- x)) \दाएं))^(\प्राइम ))\text(d)x)=-((\text(e))^(-x))+C \\\end(संरेखित)\]
आइए अब $g$ फ़ंक्शन को देखें:
$g=x\राइटएरो (g)"=1$
हम अभिन्न की गणना करते हैं:
$\begin(संरेखित करें)& \int(((\text(e))^(-x))\cdot x\,\text(d)x)=x\cdot \left(-((\text(e) ))^(-x)) \right)-\int(\left(-((\text(e))^(-x)) \right)\cdot 1\cdot \text(d)x)= \ \& =-x((\text(e))^(-x))+\int(((\text(e))^(-x))\,\text(d)x)=-x( (\text(e))^(-x))-((\text(e))^(-x))+C=-((\text(e))^(-x))\left(x +1 \दाएं)+C \\\end(संरेखित)$
इसलिए, हमने भागों द्वारा दूसरा एकीकरण किया है।
समस्या 3. गणना करें:
$\int(x\cos 3x\,\text(d)x)$
इस मामले में, हमें $(f)"$ के लिए क्या लेना चाहिए और $g$ के लिए क्या? यदि $x$ एक व्युत्पन्न के रूप में कार्य करता है, तो एकीकरण के दौरान हमें $\frac(((x)^(2)) मिलेगा )(2 )$, और पहला कारक कहीं भी गायब नहीं होगा - यह $\frac(((x)^(2)))(2)\cdot \cos 3x$ होगा, आइए कारकों को फिर से बदलें:
$\begin(संरेखित करें)& \int(x\cos 3x\,\text(d)x)=\int(\cos 3x\cdot x\,\text(d)x) \\& (f)"= \cos 3x\राइटएरो f=\int(\cos 3x\,\text(d)x)=\frac(\sin 3x)(3) \\& g=x\राइटएरो (g)"=1 \\\ अंत(संरेखित)$
हम अपनी मूल अभिव्यक्ति को फिर से लिखते हैं और भागों द्वारा एकीकरण सूत्र के अनुसार इसका विस्तार करते हैं:
\[\begin(संरेखित करें)& \int(\cos 3x\cdot x\ \text(d)x)=\frac(\sin 3x)(3)\cdot x-\int(\frac(\sin 3x) (3)\text(d)x)= \\& =\frac(x\sin 3x)(3)-\frac(1)(3)\int(\sin 3x\,\text(d)x) =\frac(x\sin 3x)(3)+\frac(\cos 3x)(9)+C \\\end(संरेखित)\]
बस, तीसरी समस्या हल हो गई।
अंत में, आइए एक और नज़र डालें भागों सूत्र द्वारा एकीकरण. हम कैसे चुनें कि कौन सा कारक व्युत्पन्न होगा और कौन सा वास्तविक कार्य होगा? यहां केवल एक ही मानदंड है: जिस तत्व को हम अलग करेंगे उसे या तो एक "सुंदर" अभिव्यक्ति देनी होगी, जो तब कम हो जाएगी, या भेदभाव के दौरान पूरी तरह से गायब हो जाएगी। इससे पाठ समाप्त होता है।
इस विषय में हम तथाकथित "भागों के सूत्र द्वारा एकीकरण" का उपयोग करके अनिश्चितकालीन अभिन्नों की गणना के बारे में विस्तार से बात करेंगे। हमें अनिश्चितकालीन अभिन्नों की एक तालिका और डेरिवेटिव की एक तालिका की आवश्यकता होगी। पहले भाग में हम जांच करेंगे मानक उदाहरण, जो अधिकतर मानक गणनाओं में पाए जाते हैं और परीक्षण. अधिक जटिल उदाहरणदूसरे भाग में चर्चा की गई।
मानक मामले में समस्या विवरण इस प्रकार है। मान लीजिए कि इंटीग्रल के अंतर्गत हमारे पास दो कार्य हैं भिन्न प्रकृति का: बहुपद और त्रिकोणमितीय फलन, बहुपद और लघुगणक, बहुपद और व्युत्क्रम त्रिकोणमितीय फलन इत्यादि। इस स्थिति में, एक फ़ंक्शन को दूसरे से अलग करना फायदेमंद होता है। मोटे तौर पर, इंटीग्रैंड को भागों में तोड़ना और प्रत्येक भाग से अलग से निपटना समझ में आता है। इसलिए नाम: "भागों द्वारा एकीकरण।" इस विधि का अनुप्रयोग निम्नलिखित प्रमेय पर आधारित है:
मान लीजिए कि फ़ंक्शन $u(x)$ और $v(x)$ कुछ अंतराल पर भिन्न हो सकते हैं, और इस अंतराल पर एक अभिन्न $\int v \ मौजूद है; दु$. फिर उसी अंतराल पर अभिन्न $\int u \; का भी अस्तित्व होता है। DV$, और निम्नलिखित समानता सत्य है:
\begin(समीकरण) \int u \; dv=u\cdot v-\int v\; डु\एंड(समीकरण)
सूत्र (1) को "भाग सूत्र द्वारा एकीकरण" कहा जाता है। कभी-कभी, उपरोक्त प्रमेय को लागू करते समय, वे "भागों द्वारा एकीकरण की विधि" का उपयोग करने के बारे में बात करते हैं। इस पद्धति का सार हमारे लिए महत्वपूर्ण होगा, जिस पर हम उदाहरणों का उपयोग करके विचार करेंगे। ऐसे कई मानक मामले हैं जिनमें सूत्र (1) स्पष्ट रूप से लागू होता है। ये ऐसे मामले हैं जो इस पृष्ठ का विषय बनेंगे। चलो $P_n(x)$ - nवाँ बहुपदडिग्री. आइए दो नियम प्रस्तुत करें:
नियम 1
फॉर्म $\int P_n(x) \ln x \;dx$, $\int P_n(x) \arcsin x \;dx$, $\int P_n(x) \arccos x \;dx$ के इंटीग्रल के लिए, $\ int P_n(x)\arctg x \;dx$, $\int P_n(x) \arcctg x \;dx$ हम $dv=P_n(x)dx$ लेते हैं।
नियम #2
फॉर्म $\int P_n(x) a^x \;dx$ ($a$ कुछ सकारात्मक संख्या है) के अभिन्न अंग के लिए, $\int P_n(x) \sin x \;dx$, $\int P_n(x ) \ cos x \;dx$, $\int P_n(x)ch x \;dx$, $\int P_n(x) sh x \;dx$ हम $u=P_n(x)$ लेते हैं।
मुझे तुरंत ध्यान देना चाहिए कि उपरोक्त प्रविष्टियों को शाब्दिक रूप से नहीं लिया जाना चाहिए। उदाहरण के लिए, फॉर्म $\int P_n(x) \ln x \;dx$ के इंटीग्रल्स में जरूरी नहीं कि बिल्कुल $\ln x$ हो। $\ln 5x$ और $\ln (10x^2+14x-5)$ दोनों वहां स्थित हो सकते हैं। वे। अंकन $\ln x$ को एक प्रकार के सामान्यीकरण के रूप में लिया जाना चाहिए।
एक और बात। ऐसा होता है कि भागों द्वारा एकीकरण सूत्र को कई बार लागू करना पड़ता है। आइए इसके बारे में उदाहरण संख्या 4 और संख्या 5 में अधिक विस्तार से बात करें। आइए अब सीधे सामान्य समस्याओं को हल करने की ओर बढ़ते हैं। जिन समस्याओं का स्तर मानक से थोड़ा अधिक है, उनके समाधान पर दूसरे भाग में चर्चा की गयी है।
उदाहरण क्रमांक 1
$\int (3x+4) \cos (2x-1) \; खोजें dx$.
समाकलन के नीचे बहुपद $3x+4$ और त्रिकोणमितीय फलन $\cos (2x-1)$ है। यह सूत्र को लागू करने का एक उत्कृष्ट मामला है, तो आइए भागों द्वारा दिए गए अभिन्न अंग को लें। सूत्र के लिए आवश्यक है कि अभिन्न $\int (3x+4) \cos (2x-1)\; dx$ को $\int u\ के रूप में दर्शाया गया था; डीवी$. हमें $u$ और $dv$ के लिए अभिव्यक्तियाँ चुनने की आवश्यकता है। हम $3x+4$ को $u$ के रूप में ले सकते हैं, फिर $dv=\cos (2x-1)dx$। हम $u=\cos (2x-1)$ ले सकते हैं, फिर $dv=(3x+4)dx$। करने के लिए सही पसंदचलो की ओर मुड़ें। दिया गया अभिन्न $\int (3x+4) \cos (2x-1)\; dx$ $\int P_n(x) \cos x \;dx$ के रूप में आता है (हमारे अभिन्न अंग में बहुपद $P_n(x)$ का रूप $3x+4$ है)। के अनुसार, आपको $u=P_n(x)$ चुनना होगा, यानी। हमारे मामले में $u=3x+4$. चूँकि $u=3x+4$, तो $dv=\cos(2x-1)dx$.
हालाँकि, केवल $u$ और $dv$ चुनना पर्याप्त नहीं है। हमें $du$ और $v$ के मानों की भी आवश्यकता होगी। चूँकि $u=3x+4$, तो:
$$ du=d(3x+4)=(3x+4)"dx=3dx.$$
अब आइए फ़ंक्शन $v$ को देखें। चूँकि $dv=\cos(2x-1)dx$, तो अनिश्चितकालीन अभिन्न की परिभाषा के अनुसार हमारे पास है: $ v=\int \cos(2x-1)\; dx$. आवश्यक अभिन्न को खोजने के लिए, हम निम्नलिखित को अवकल चिह्न पर लागू करते हैं:
$$ v=\int \cos(2x-1)\; dx=\frac(1)(2)\cdot \int \cos(2x-1)d(2x-1)=\frac(1)(2)\cdot \sin(2x-1)+C=\frac (\sin(2x-1))(2)+C. $$
हालाँकि, हमें फ़ंक्शन $v$ के संपूर्ण अनंत सेट की आवश्यकता नहीं है, जिसे सूत्र $\frac(\sin(2x-1))(2)+C$ द्वारा वर्णित किया गया है। हम कुछ की जरूरत है एकइस सेट से कार्य करें. आवश्यक फ़ंक्शन प्राप्त करने के लिए, आपको $C$ के स्थान पर कुछ संख्या प्रतिस्थापित करनी होगी। बेशक, सबसे आसान तरीका $C=0$ को प्रतिस्थापित करना है, जिससे $v=\frac(\sin(2x-1))(2)$ प्राप्त होता है।
तो, आइए उपरोक्त सभी को एक साथ रखें। हमारे पास है: $u=3x+4$, $du=3dx$, $dv=\cos(2x-1)dx$, $v=\frac(\sin(2x-1))(2)$. यह सब इसमें प्रतिस्थापित करना दाहिनी ओरहमारे पास सूत्र होंगे:
$$ \int (3x+4) \cos (2x-1) \; dx=(3x+4)\cdot\frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2)\cdot 3dx. $$
वास्तव में, जो कुछ बचा है, वह $\int\frac(\sin(2x-1))(2)\cdot 3dx$ खोजना है। स्थिरांक (अर्थात् $\frac(3)(2)$) को अभिन्न चिह्न के बाहर लेते हुए और इसे अवकल चिह्न के अंतर्गत प्रस्तुत करने की विधि को लागू करने पर, हम प्राप्त करते हैं:
$$ (3x+4)\cdot \frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2)\cdot 3dx= \frac((3x+ 4) )\cdot\sin(2x-1))(2)-\frac(3)(2)\int \sin(2x-1) \;dx= \\ =\frac((3x+4)\cdot \ पाप(2x-1))(2)-\frac(3)(4)\int \sin(2x-1) \;d(2x-1)= \frac((3x+4)\cdot\sin ( 2x-1))(2)-\frac(3)(4)\cdot (-\cos (2x-1))+C=\\ =\frac((3x+4)\cdot\sin(2x - 1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C. $$
तो $\int (3x+4) \cos (2x-1) \; dx=\frac((3x+4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C$. संक्षिप्त रूप में, समाधान प्रक्रिया इस प्रकार लिखी गई है:
$$ \int (3x+4) \cos (2x-1) \; dx=\बाएं | \begin(संरेखित) और u=3x+4; \; du=3xdx.\\ & dv=\cos(2x-1)dx; \; v=\frac(\sin(2x-1))(2). \end(संरेखित) \दाएं |=\\ =(3x+4)\cdot\frac(\sin(2x-1))(2)-\int \frac(\sin(2x-1))(2) \cdot 3dx= \frac((3x+4)\cdot\sin(2x-1))(2)-\frac(3)(2)\int \sin(2x-1) \;dx=\\ = \frac((3x+4)\cdot\sin(2x-1))(2)-\frac(3)(4)\cdot (-\cos (2x-1))+C= \frac((3x) +4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot\cos (2x-1)+C. $$
अनिश्चितकालीन अभिन्न अंग भागों द्वारा पाया गया है; जो कुछ बचा है वह उत्तर लिखना है।
उत्तर: $\int (3x+4) \cos (2x-1) \; dx=\frac((3x+4)\cdot\sin(2x-1))(2)+\frac(3)(4)\cdot \cos (2x-1)+C$.
मेरा मानना है कि यहां एक प्रश्न है, इसलिए मैं इसे तैयार करने और उत्तर देने का प्रयास करूंगा।
हमने बिल्कुल $u=3x+4$ और $dv=\cos(2x-1)dx$ क्यों लिया? हाँ, अभिन्न का समाधान हो गया है। लेकिन शायद अगर हम $u=\cos (2x-1)$ और $dv=(3x+4)dx$ लेते तो इंटीग्रल भी मिल जाता!
नहीं, अगर हम $u=\cos (2x-1)$ और $dv=(3x+4)dx$ लेते हैं, तो इससे कुछ भी अच्छा नहीं होगा - इंटीग्रल को सरल नहीं बनाया जाएगा। स्वयं निर्णय करें: यदि $u=\cos(2x-1)$, तो $du=(\cos(2x-1))"dx=-2\sin(2x-1)dx$। इसके अलावा, चूँकि $ dv =(3x+4)dx$, फिर:
$$ v=\int (3x+4) \; dx=\frac(3x^2)(2)+4x+C.$$
$C=0$ लेने पर, हमें $v=\frac(3x^2)(2)+4x$ मिलता है। आइए अब $u$, $du$, $v$ और $dv$ के पाए गए मानों को सूत्र में प्रतिस्थापित करें:
$$ \int (3x+4) \cos (2x-1) \; dx=\cos (2x-1)\cdot \left(\frac(3x^2)(2)+4x \right) - \int \left(\frac(3x^2)(2)+4x \right) \cdot (-2\sin(2x-1)dx)=\\ =\cos (2x-1)\cdot \left(\frac(3x^2)(2)+4x \right) +2\cdot\ int \left(\frac(3x^2)(2)+4x \right) \sin(2x-1)\;dx $$
और हम क्या करने आये हैं? हम इंटीग्रल $\int \left(\frac(3x^2)(2)+4x \right) \sin(2x-1)\;dx$ पर आ गए, जो स्पष्ट रूप से मूल इंटीग्रल $\int से अधिक जटिल है (3x+4 ) \cos (2x-1) \; dx$. इससे पता चलता है कि $u$ और $dv$ का चुनाव ख़राब तरीके से किया गया था। भागों के सूत्र द्वारा एकीकरण को लागू करने के बाद, परिणामी अभिन्न अंग मूल की तुलना में सरल होना चाहिए। भागों द्वारा अनिश्चितकालीन समाकलन ज्ञात करते समय, हमें इसे सरल बनाना चाहिए, जटिल नहीं, इसलिए यदि सूत्र (1) लागू करने के बाद समाकलन अधिक जटिल हो जाता है, तो $u$ और $dv$ का चुनाव गलत तरीके से किया गया था।
उदाहरण संख्या 2
$\int (3x^4+4x-1) \ln 5x \; खोजें dx$.
समाकलन के नीचे एक बहुपद है (अर्थात $3x^4+4x-1$) और $\ln 5x$। यह मामला के अंतर्गत आता है, तो आइए भागों द्वारा अभिन्न को लें। दिए गए इंटीग्रल की संरचना इंटीग्रल $\int P_n(x) \ln x\ के समान है; dx$. फिर से, जैसा कि उदाहरण संख्या 1 में है, हमें इंटीग्रैंड $(3x^4+4x-1) \ln 5x \; के कुछ भाग का चयन करना होगा। dx$ को $u$ के रूप में, और कुछ भाग को $dv$ के रूप में। के अनुसार, आपको $dv=P_n(x)dx$ चुनना होगा, यानी। हमारे मामले में $dv=(3x^4+4x-1)dx$. यदि व्यंजक से $(3x^4+4x-1) \ln 5x \; dx$ "हटाएं" $dv=(3x^4+4x-1)dx$, तो $\ln 5x$ रहेगा - यह फ़ंक्शन $u$ होगा। तो, $dv=(3x^4+4x-1)dx$, $u=\ln 5x$. सूत्र को लागू करने के लिए, हमें $du$ और $v$ की भी आवश्यकता है। चूँकि $u=\ln 5x$, तो:
$$ du=d(\ln 5x)=(\ln 5x)"dx=\frac(1)(5x)\cdot 5 dx=\frac(1)(x)dx. $$
आइए अब फ़ंक्शन $v$ ढूंढें। चूँकि $dv=(3x^4+4x-1)dx$, तो:
$$ v=\int(3x^4+4x-1)\; dx=\frac(3x^5)(5)+2x^2-x+C. $$
$\frac(3x^5)(5)+2x^2-x+C$ फ़ंक्शन के पूरे पाए गए अनंत सेट में से हमें एक को चुनना होगा। और ऐसा करने का सबसे आसान तरीका $C=0$ लेना है, यानी। $v=\frac(3x^5)(5)+2x^2-x$. फॉर्मूला लागू करने के लिए सब कुछ तैयार है. आइए मानों को प्रतिस्थापित करें $u=\ln 5x$, $du=\frac(1)(x)dx$, $v=\frac(3x^5)(5)+2x^2-x$ और $dv=(3x^4+4x-1)dx$ हमारे पास होगा:
$$ \int (3x^4+4x-1) \ln 5x \; dx=\बाएं | \begin(संरेखित) और u=\ln 5x; \; du=\frac(1)(x)dx.\\ & dv=(3x^4+4x-1)dx; \; v=\frac(3x^5)(5)+2x^2-x. \end(संरेखित) \दाएं |=\\ =\ln 5x \cdot \left (\frac(3x^5)(5)+2x^2-x \right)-\int \left (\frac(3x^ 5)(5)+2x^2-x \right)\cdot \frac(1)(x)dx=\\ =\left (\frac(3x^5)(5)+2x^2-x \right )\cdot\ln 5x -\int \left (\frac(3x^4)(5)+2x-1 \right)dx=\\ =\left (\frac(3x^5)(5)+2x^ 2-x \right)\cdot\ln 5x - \left (\frac(3x^5)(25)+x^2-x \right)+C=\\ =\left (\frac(3x^5) (5)+2x^2-x \right)\cdot\ln 5x - \frac(3x^5)(25)-x^2+x+C. $$
उत्तर: $\int (3x^4+4x-1) \ln 5x \; dx=\left (\frac(3x^5)(5)+2x^2-x \right)\cdot\ln 5x - \frac(3x^5)(25)-x^2+x+C$.
उदाहरण संख्या 3
$\int \arccos x\ ढूंढें; dx$.
इस इंटीग्रल की संरचना $\int P_n(x) \arccos x \;dx$ है, जो के अंतर्गत आती है। मैं समझता हूं कि एक उचित प्रश्न तुरंत उठेगा: "दिए गए अभिन्न $\int\arccos x \; dx$ में उन्होंने बहुपद $P_n(x)$ को कहां छिपाया है? वहां कोई बहुपद नहीं है, केवल आर्ककोसाइन है और बस इतना ही!" ” हालाँकि, वास्तव में, न केवल आर्क कोसाइन इंटीग्रल के अंतर्गत स्थित है। मैं अभिन्न $\int arccos x\ प्रस्तुत करूंगा; dx$ इस रूप में: $\int 1\cdot\arccos x \; dx$. सहमत हूँ कि एक से गुणा करने पर समाकलन नहीं बदलेगा। यह इकाई $P_n(x)$ है। वे। $dv=1\cdot dx=dx$. और $u$ के रूप में (के अनुसार) हम $\arccos x$ लेते हैं, यानी। $u=\arccos x$. हम $du$ और $v$ मान ढूंढते हैं, जो पिछले उदाहरणों की तरह ही सूत्र में शामिल हैं:
$$ du=(\arccos x)"dx=-\frac(1)(\sqrt(1-x^2))dx;\\ v=\int 1\; dx=x+C. $$
पिछले उदाहरणों की तरह, $C=0$ मानने पर हमें $v=x$ मिलता है। सभी पाए गए मापदंडों को सूत्र में प्रतिस्थापित करने पर, हमारे पास निम्नलिखित होंगे:
$$ \int \arccos x \; dx=\बाएं | \begin(संरेखित) और u=\arccos x; \; du=-\frac(1)(\sqrt(1-x^2))dx.\\ & dv=dx; \; वी=एक्स. \end(संरेखित) \दाएं |=\\ =\arccos x \cdot x-\int x\cdot \left(-\frac(1)(\sqrt(1-x^2))dx \right)= \ आर्ककोस x \cdot x+\int \frac(xdx)(\sqrt(1-x^2))=\\ =x\cdot\arccos x-\frac(1)(2)\cdot\int (1-x ^2)^(-\frac(1)(2))d(1-x^2)= =x\cdot\arccos x-\frac(1)(2)\cdot\frac((1-x^ 2)^(\frac(1)(2)))(\frac(1)(2))+C=\\ =x\cdot\arccos x-\sqrt(1-x^2)+C. $$
उत्तर: $\int\arccos x\; dx=x\cdot\arccos x-\sqrt(1-x^2)+C$.
उदाहरण संख्या 4
$\int (3x^2+x) e^(7x) \ खोजें; dx$.
इस उदाहरण में, भागों द्वारा एकीकरण सूत्र को दो बार लागू करना होगा। इंटीग्रल $\int (3x^2+x) e^(7x) \; dx$ की संरचना $\int P_n(x) a^x \;dx$ है। हमारे मामले में, $P_n(x)=3x^2+x$, $a=e$. हमारे अनुसार: $u=3x^2+x$. तदनुसार, $dv=e^(7x)dx$.
$$ du=(3x^2+x)"=(6x+1)dx;\\ v=\int e^(7x)\;dx=\frac(1)(7)\cdot \int e^( 7x)\;d(7x)=\frac(1)(7)\cdot e^(7x)+C=\frac(e^(7x))(7)+C $$.
पुनः, पिछले उदाहरणों की तरह, $C=0$ मानते हुए, हमारे पास है: $v=\frac(e^(7x))(7)$.
$$ \int (3x^2+x) e^(7x) \; dx=\बाएं | \begin(संरेखित) और u=3x^2+x; \; du=(6x+1)dx.\\ & dv=e^(7x)dx; \; v=\frac(e^(7x))(7). \end(संरेखित) \दाएं |=\\ =(3x^2+x)\cdot\frac(e^(7x))(7)-\int \frac(e^(7x))(7)\cdot (6x+1)dx= \frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \int (6x+1) e^(7x)\ ;dx. $$
हम अभिन्न $\int (6x+1) e^(7x)\;dx$ पर आ गए हैं, जिसे फिर से भागों में लिया जाना चाहिए। $u=6x+1$ और $dv=e^(7x)dx$ लेने पर हमारे पास है:
$$ \frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \int (6x+1) e^(7x)\;dx=\left | \begin(संरेखित) और u=6x+1; \; du=6dx.\\ & dv=e^(7x)dx; \; v=\frac(e^(7x))(7). \end(संरेखित) \दाएं |=\\ =\frac((3x^2+x)e^(7x))(7)-\frac(1)(7)\cdot \left ((6x+1) \cdot\frac(e^(7x))(7) - \int\frac(e^(7x))(7)\cdot 6\;dx \right)=\\ =\frac((3x^2+) x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6)(49)\cdot\int\ e^(7x)\; dx=\\ =\frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6)(49) )\cdot\frac(e^(7x))(7)+C=\\ =\frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e ^(7x))(49) +\frac(6\; e^(7x))(343)+C. $$
कोष्ठक खोलकर और शब्दों को पुनर्व्यवस्थित करके परिणामी उत्तर को सरल बनाया जा सकता है:
$$ \frac((3x^2+x)e^(7x))(7) -\frac((6x+1)e^(7x))(49) +\frac(6\; e^(7x) ))(343)+C=e^(7x)\cdot \left(\frac(3x^2)(7)+\frac(x)(49)-\frac(1)(343) \right)+ सी। $$
उत्तर: $\int (3x^2+x) e^(7x) \; dx=e^(7x)\cdot \left(\frac(3x^2)(7)+\frac(x)(49)-\frac(1)(343) \right)+C$.
उदाहरण क्रमांक 5
$\int (x^2+5)\sin(3x+1) \; खोजें dx$.
यहां, पिछले उदाहरण की तरह, भागों द्वारा एकीकरण दो बार लागू किया जाता है। विस्तृत स्पष्टीकरण पहले दिए गए थे, इसलिए मैं केवल समाधान दूंगा:
$$ \int (x^2+5)\sin(3x+1) \; dx=\बाएं | \begin(संरेखित) और u=x^2+5; \; du=2xdx.\\ & dv=\sin(3x+1)dx; \; v=-\frac(\cos(3x+1))(3). \end(संरेखित) \right |=\\ =(x^2+5)\cdot \left(-\frac(\cos(3x+1))(3) \right)-\int\left(-\ frac(\cos(3x+1))(3) \right)\cdot 2xdx=\\ = -\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac (2)(3)\int x\cos(3x+1)dx= \left | \begin(संरेखित) और u=x; \; du=dx.\\ & dv=\cos(3x+1)dx; \; v=\frac(\sin(3x+1))(3). \end(संरेखित) \दाएं |=\\ =-\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac(2)(3)\cdot \left( x\cdot\frac(\sin(3x+1))(3)-\int\frac(\sin(3x+1))(3)dx \right)=\\ =-\frac((x^2) +5)\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac(2)(9)\cdot\int\sin(3x+ 1) )dx=\\ =-\frac((x^2+5)\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac ( 2)(9)\cdot \left(-\frac(\cos(3x+1))(3)\right)+C=\\ = -\frac((x^2+5)\cdot\cos ( 3x+1))(3) +\frac(2x\sin(3x+1))(9)+\frac(2\cos(3x+1))(27)+C=\\ =-\frac ( x^2\cdot\cos(3x+1))(3)-\frac(5\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9 ) +\frac(2\cos(3x+1))(27)+C=\\ =-\frac(x^2\cdot\cos(3x+1))(3) +\frac(2x\sin ( 3x+1)(9)-\frac(43\cos(3x+1))(27)+C. $$
उत्तर: $\int (x^2+5)\sin(3x+1) \; dx=-\frac(x^2\cdot\cos(3x+1))(3) +\frac(2x\sin(3x+1))(9)-\frac(43\cos(3x+1) )(27)+सी$.
कुछ गैर-मानक मामलों में भागों द्वारा एकीकरण की विधि का अनुप्रयोग जो नियम संख्या 1 और संख्या 2 के अधीन नहीं हैं, में दिया जाएगा







